Veritasium hat ein Video auf YouTube veröffentlich in dem es um ein merkwürdiges Experiment geht.
100 Gefangene werden nacheinander in einen Raum geschickt. In diesem Raum befinden sich 100 Boxen mit den Zahlen eins bis 100. In jeder Kiste ist eine Zufällige Zahl von 1 bis 100 Jeder Gefangene darf 50 Kisten öffnen und wenn er seine eigene Nummer darin findet, hat er die Aufgabe bestanden und der nächste Gefangene muss vortreten. Jeder Gefangene muss den Raum genau so hinterlassen, wie er ihn vorgefunden hat und darf danach nicht mehr mit den übrigen Gefängnisinsassen kommunzieren. Wenn auch nur einer seine Zahl nicht findet, werden alle exekutiert.
Diese Rätsel müssen immer so blutrünstig sein.
Die Frage: Gibt es eine Strategie, auf die sich die Insassen einigen können, bevor der erste den Raum betritt, durch die sich ihre Chancen erhöhen?
Die vorgeschlagene Lösung: Jeder Gefangene öffnet zunächst die Kiste auf der seine eigene Nummer steht. Each prisoner opens the box with his number as the label first and then moves to the box with the number he finds inside that box.
Zum Beispiel: Gefangener nummer 10 geht in den Raum, öffnet Kiste nummer 10 und gewinnt. Wenn er nicht die 10 vorfindet, öffnet er als nächstes die Kiste, deren Nummer sich in der zuvor geöffneten Kiste befindet und so weiter.
Als mir diese Lösung präsentiert wurde, dachte ich zuerst: Das is sicher eine theoretische Lösung, die in Wirklichkeit keinen Einfluss hat. Ich habe nicht überprüft wie niedrig die Gewinnchancen sind, wenn alle Kisten zufällig geöffnet werden, ich gehe davon aus, dass (1/2)^100 stimmt oder die Zahl doch zumindest äußerst niedig sein dürfte.
Hier ist das Skript, das ausdruckt wie oft alle Gefangenen mit der vorgeschlagenen Lösung gewinnen.
import numpy as np
import random
import time
print(100*"=")
prisoners = 100 # set number of prisoners here
def run(l):
for i in range(prisoners):
success = send_prisoner(l, i) #
if not success:
#print("All dead, accomplished:", i)
return False, i # i prisoners found their box before 1 failed
return True, prisoners
def send_prisoner(l, prisoner):
# let 1 prisoner search the boxes
next_box = prisoner # start with the box with index prisoner
for i in range(prisoners // 2): # each prisoner can check half the amount of boxes as there are prisoners
#print("Checking", next_box, "found:", l[next_box]) #uncomment to check if they march in loops
if l[next_box] == prisoner:
#print("Found it, tries", i) # uncomment to see how many tries it took each prisoner
return True
next_box = l[next_box]
return False
def get_boxes():
boxes = []
for i in range(prisoners):
boxes.append(i)
random.shuffle(boxes)
return boxes
# returns as many boxes as there are prisoners
boxes = np.arange(prisoners) # get a list of the numbers [0 ; prisoners -1]
np.random.shuffle(boxes) #shuffle the numbers inside the boxes
return boxes
def main():
successes = 0
total_successes = 0
start_time = time.time()
n = 1000 # how many times the warden gets his sadism on
for i in range(n):
l = get_boxes()
success, total = run(l) # run 1 experiment
#print("Run no:", i, "successes:", total)
total_successes += total
if success:
successes += 1
end_time = time.time()
win_ratio = successes / n
total_completed = total_successes / (prisoners * n)
print("Total prisoners that succeeded", total_successes, "out of: ", (prisoners * n), "=>", total_completed)
print("Win ratio:", str(round(win_ratio * 100, 3)) + '%')
print("Method took:", end_time - start_time) # so you can plan ahead how much time it would take to increase either n or prisoners
if __name__ == "__main__":
main()Das Skript weiter unten erzeugt automatisch Graphen, von denen 4 hier präsentiert werden.
100,000 durchläufe erzeugten folgendende Zahlen:
Gefangene: 2, Erfolgsrate 0.49721
Gefangene: 20, Erfolgsrate 0.32954
Gefangene: 50, Erfolgsrate 0.31907
Gefangene: 100, Erfolgsrate 0.31063
Gefangene: 200, Erfolgsrate 0.30901
Gefangene: 500, Erfolgsrate 0.30874
Gefangene: 1000, Erfolgsrate 0.30913
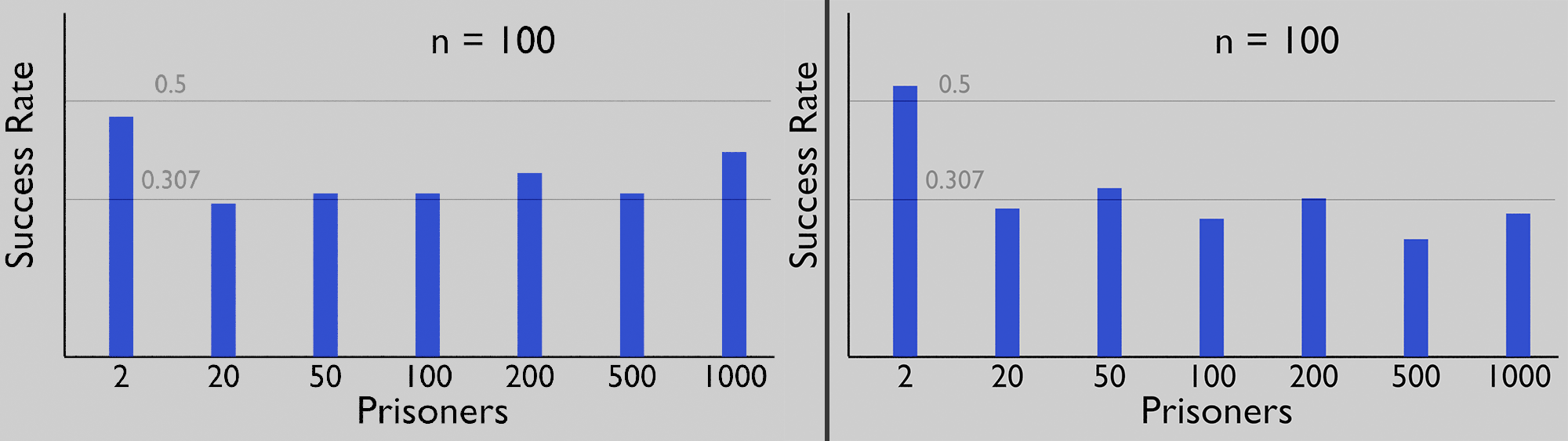
Wie zu erwarten reicht es nicht aus, das Experiment 100 mal zu wiederholen um statistisch relevante Aussagen treffen zu können. Das wäre ein wenig wie 6 mal zu würfeln und alle Zahlen von 1 bis 6 genau einmal zu erwarten.
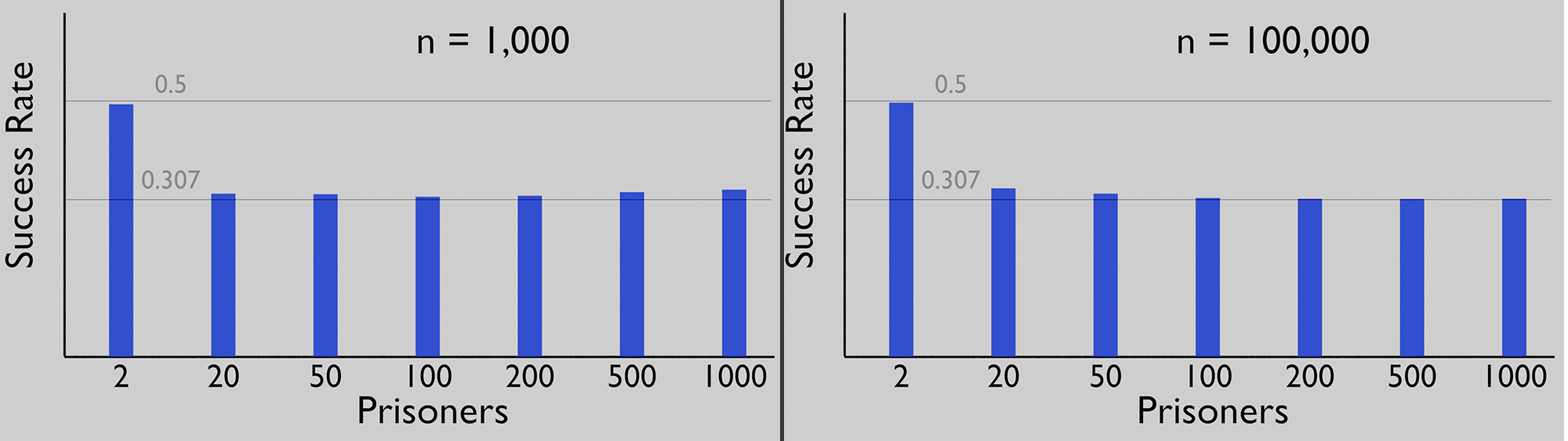
1.000 Iterationen bringen uns dem tatsächlichen Ergebnis etwas näher und 100.000 Durchläufe sollten genügen, um statistisch zu belegen, dass die oben vorgeschlagene Methode die Chancen von nahe null auf über 30% erhöht. Sieh einer an.
Und da dies hier nicht BlenderDiplom wäre, wenn wir das Script, mit dem man diese Ergebnisse grafisch darstellen kann nicht einfügen würden:
import random
import time
from bpy import data as D
from bpy import context as C
from mathutils import Vector
print(100*"=")
def run(l, prisoners):
for i in range(prisoners):
success = send_prisoner(l, i) #
if not success:
#print("All dead, accomplished:", i)
return False, i # i prisoners found their box before 1 failed
return True, prisoners
def send_prisoner(l, prisoner):
# let 1 prisoner search the boxes
next_box = prisoner # start with the box with index prisoner
length = len(l) // 2
for i in range(length): # each prisoner can check half the amount of boxes as there are prisoners
#print("Checking", next_box, "found:", l[next_box]) #uncomment to check if they march in loops
if l[next_box] == prisoner: # number inside the box equals the number of the current prisoner
#print("Found it, tries", i) # uncomment to see how many tries it took each prisoner
return True
next_box = l[next_box]
return False
def get_boxes(prisoners):
# returns as many boxes as there are prisoners
boxes = []
for i in range(prisoners):
boxes.append(i)
random.shuffle(boxes)
return boxes
def run_experiment(prisoners, n):
team_successes = 0 # number of times all prisoners succeded
start_time = time.time()
results = []
for i in range(n):
l = get_boxes(prisoners)
success, total = run(l, prisoners) # run 1 experiment
#print("Run no:", i, "successes:", total)
if success:
team_successes += 1
win_ratio = team_successes / n
return win_ratio
def plot(results, distance):
mesh = D.meshes['Plane'] # the base mesh for the bar, add a plane and scale it in Edit Mode
collection = D.collections['Plot']
txt_mat = None
bar_mat = None
if not 'Label' in D.materials:
txt_mat = D.materials.new('Label')
else:
txt_mat = D.materials['Label']
for i, result in enumerate(results):
prisoners = result['prisoners']
print("Prisoners", prisoners, "Win rate", result['win_ratio'])
label = str(prisoners)
txt = D.curves.new(type="FONT", name = 'Label-' + label) # need to use a font curve as object data
txt.body = label
txt.align_x = 'CENTER'
txt_ob = D.objects.new('Label-' + label, txt) # curve here, text does not work directly
txt_ob.data.materials.append(txt_mat) # so you can change the appearance of all labels at once
x = i * distance # evenly space the results
txt_ob.location = Vector((x, -1.2, 0)) #hardcoded values that fit the current setup
txt_scale = 1.3
txt_ob.scale = Vector((txt_scale, txt_scale, txt_scale))
bar = D.objects.new('Bar-' + label, mesh)
bar.scale = Vector((1, result['win_ratio'] * 20, 1))
bar.location = Vector((x, 0, 0))
collection.objects.link(txt_ob) # link the objects to the collection
collection.objects.link(bar)
def main():
start_time = time.time()
results = []
current_prisoners = [2, 20, 50, 100, 200, 500, 1000]
n = 100 # how many times the warden gets his sadism on
for prisoners in current_prisoners:
win_ratio = run_experiment(prisoners, n)
result = { # use a struct to link the current no of prisoners to their win ratio
'prisoners' : prisoners,
'win_ratio' : win_ratio
}
results.append(result)
print(prisoners, "prisoners:", win_ratio)
end_time = time.time()
print("Calculations took:", end_time - start_time) # in sec so you can plan ahead how much time it would take to increase either n or prisoners
distance = 4 # spacing between 2 bars
plot(results, distance)
if __name__ == "__main__":
main()