Blender 2.8 und Animation Nodes lassen Mathe weniger einschüchternd wirken. Im ersten Teil dieser Serie zeigt Frederik Steinmetz, wie man eine mathematische Formel in einen Animation Nodes Tree umwandelt, der die berühmte Kleeblattschlinge erzeugt.
Computergrafik und Mathematik gehen Hand in Hand. Die hübschen Bilder, die mit Hilfe von CGI-Programmen wie Blender erstellt werden, sind nur möglich, weil der Computer viele mathematische Berechnungen durchführt. Diese Komplexität wird vor dem Nutzer verborgen, und Blender bildet da keine Ausnahme. Es gibt jedoch ein paar Stellen, an denen man tiefer graben kann, nämlich Compositing, Shading und die Animation Nodes. Und Driver natürlich nicht vergessen.
Da sich Mathematik und Kunst in der Computergrafik begegnen, liegt es doch nahe, ein wenig Mathematik zu lernen, während man hübsche Bilder erzeugt (oder anders herum). Frederik Steinmetz zeigt euch, wie man Animation Nodes für prozedurale Modellierung nutzen kann. Als Beispiel dient die berühmte Kleeblattschlinge. Finde heraus, wie man eine mathematische Formel in eine Gruppe von Nodes umwandelt, die man einsetzen kann, um ein Objekt auf einem Pfad zu bewegen oder direkt eine eine Bézierkurve zu erzeugen. Der finale Node Tree sieht folgendermaßen aus:
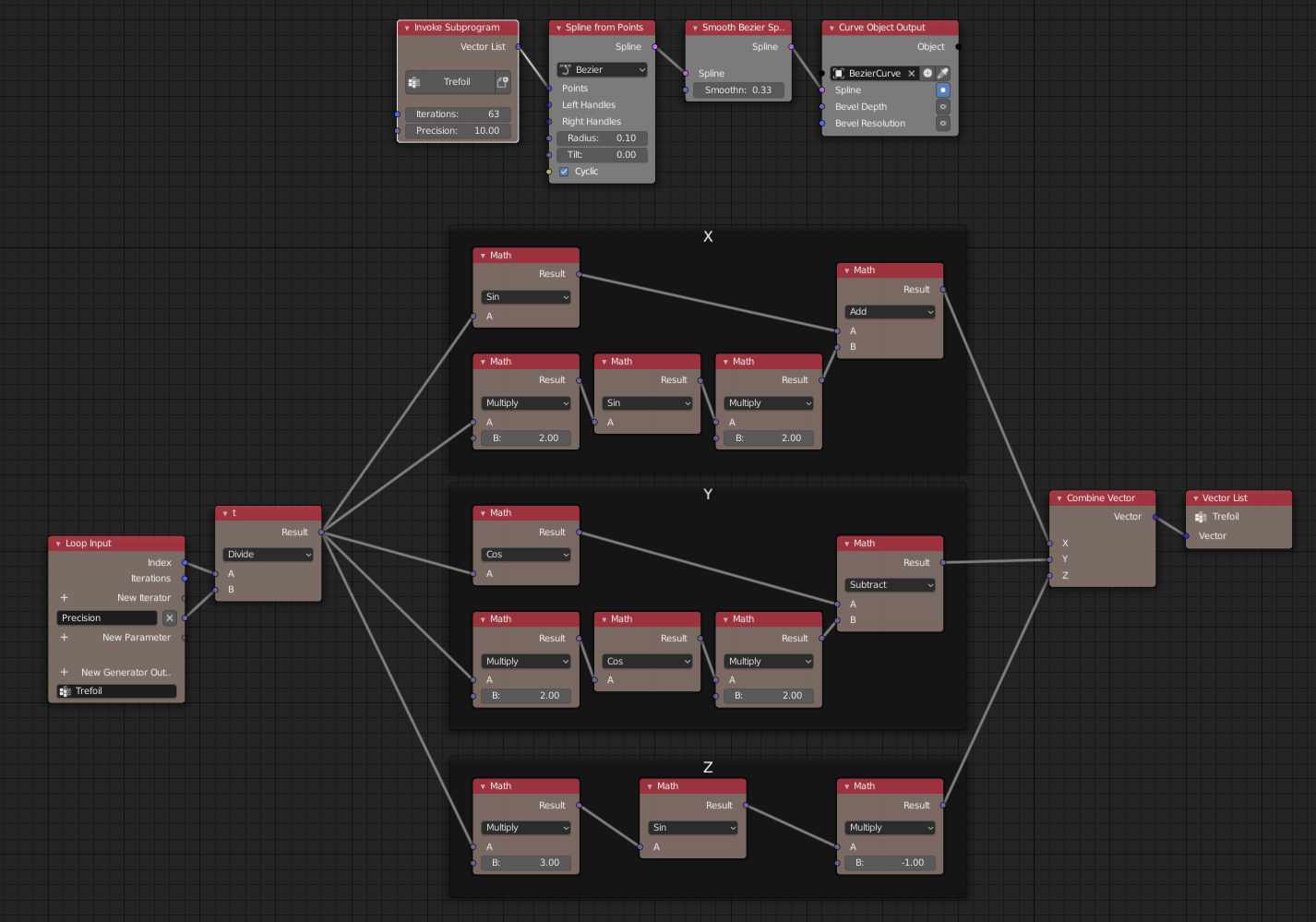
Patreon-Unterstützer können die .blend zum Tutorial herunterladen.